Poisson Distribution: A Comprehensive Guide To Understanding Data With Discrete Events
Poisson distribution is a fundamental tool for modeling and analyzing data involving discrete events that occur at a constant average rate. It is named after the French mathematician Siméon Denis Poisson who first introduced it in 1837. The Poisson distribution has wide applications in fields like queuing theory, insurance, reliability engineering, and many others.
Editor's Notes: Poisson Distribution: A Comprehensive Guide To Understanding Data With Discrete Events has been published today, March 8, 2023. This topic is important to read because it provides a detailed overview of the Poisson distribution, its properties, and its applications. The guide will be useful for researchers, practitioners, and students who work with data involving discrete events.
To help our target audience make the right decision, we have done some analysis, digging information, made a Poisson Distribution: A Comprehensive Guide To Understanding Data With Discrete Events. This guide will provide you with everything you need to know about the Poisson distribution, from its definition and properties to its applications and limitations.
Key Differences
The Poisson distribution is different from other probability distributions in the following ways:
| Characteristic | Poisson Distribution | Other Probability Distributions |
|---|---|---|
| Number of events | Discrete | Can be discrete or continuous |
| Event rate | Constant | Can vary over time |
| Applications | Modeling discrete events that occur at a constant average rate | Modeling a wide variety of phenomena |
Key Takeaways
- The Poisson distribution is a powerful tool for modeling and analyzing data involving discrete events that occur at a constant average rate.
- The Poisson distribution has wide applications in fields like queuing theory, insurance, reliability engineering, and many others.
- The guide provides a comprehensive overview of the Poisson distribution, its properties, and its applications.
- The guide will be useful for researchers, practitioners, and students who work with data involving discrete events.

Free Poisson Distribution Templates For Google Sheets And Microsoft - Source slidesdocs.com
Main Article Topics
The guide covers the following main topics:
- Definition and properties of the Poisson distribution
- Applications of the Poisson distribution
- Limitations of the Poisson distribution
- Alternatives to the Poisson distribution
FAQ About Poisson Distribution
This FAQ section provides answers to common questions and misconceptions regarding the Poisson distribution, offering a comprehensive understanding of this important probability distribution model.
Question 1: What is the Poisson distribution?
The Poisson distribution is a discrete probability distribution that describes the number of events occurring within a fixed interval of time or space, where the probability of an event occurring is assumed to be constant. It is commonly used to model scenarios where events occur randomly and independently.
Question 3: What are the assumptions of the Poisson distribution?
The Poisson distribution assumes that events occur independently of each other and at a constant average rate. Additionally, it assumes that the number of events within the interval is finite and that the probability of two or more events occurring simultaneously is negligible.
Question 4: What is the relationship between the Poisson distribution and the exponential distribution?
The Poisson distribution can be derived from the exponential distribution, which describes the time between events. The average time between events in the Poisson distribution is equal to 1/λ.
Question 5: How can the Poisson distribution be used in practice?
The Poisson distribution has various applications, including modeling the number of phone calls received by a call center per hour, the number of defects found in a manufactured product, and the number of radioactive particles emitted by a substance. It is widely used in fields such as statistics, quality control, and insurance.
Question 6: What are the limitations of the Poisson distribution?
The Poisson distribution assumes a constant event rate, which may not always be realistic in practice. Additionally, it is only applicable when the events are independent and when the probability of multiple events occurring simultaneously is negligible.
Tips

Discrete Data - Cuemath - Source www.cuemath.com
The Poisson distribution is a powerful tool for analyzing data with discrete events. To effectively use the Poisson distribution, here are some practical tips to enhance your understanding and applications:
Tip 1: Determine Event Independence
The Poisson distribution assumes that events occur independently of one another. Check that the events you are analyzing do not depend on or influence each other's occurrence. If there is dependence, consider using alternative probability models.
Tip 2: Calculate the Mean Rate
The mean rate (λ) is a crucial parameter in the Poisson distribution. It represents the average number of events that occur in a given time interval or area. Accurately estimating the mean rate is essential for reliable modeling.
Tip 3: Model Rare Events
The Poisson distribution is well-suited for modeling rare events whose occurrence is not predictable but has a constant mean rate. It provides a framework for understanding the probability of observing a specific number of events within a defined interval.
Tip 4: Use Tables and Calculators
Poisson distribution tables and online calculators can simplify calculations and save time. These resources provide precomputed probabilities for various values of λ and the number of events. They can also be used for hypothesis testing and confidence interval estimation.
Tip 5: Explore Applications
Consider the broad range of applications where Poisson distribution can be applied. It is commonly used in fields such as quality control, insurance, transportation, and healthcare research. Understanding the practical applications will enhance your problem-solving and decision-making abilities.
In summary, by applying these tips, you will gain a deeper understanding of the Poisson distribution and its applications. Poisson Distribution: A Comprehensive Guide To Understanding Data With Discrete Events Embracing these principles will empower you to effectively analyze data, draw meaningful conclusions, and make informed decisions.
Poisson Distribution: A Comprehensive Guide To Understanding Data With Discrete Events
The Poisson distribution is a discrete probability distribution that models the number of events occurring independently and at a constant average rate within a fixed interval of time or space. It is widely used in various fields to analyze and predict the occurrence of events such as customer arrivals, radioactive decays, and website visits.
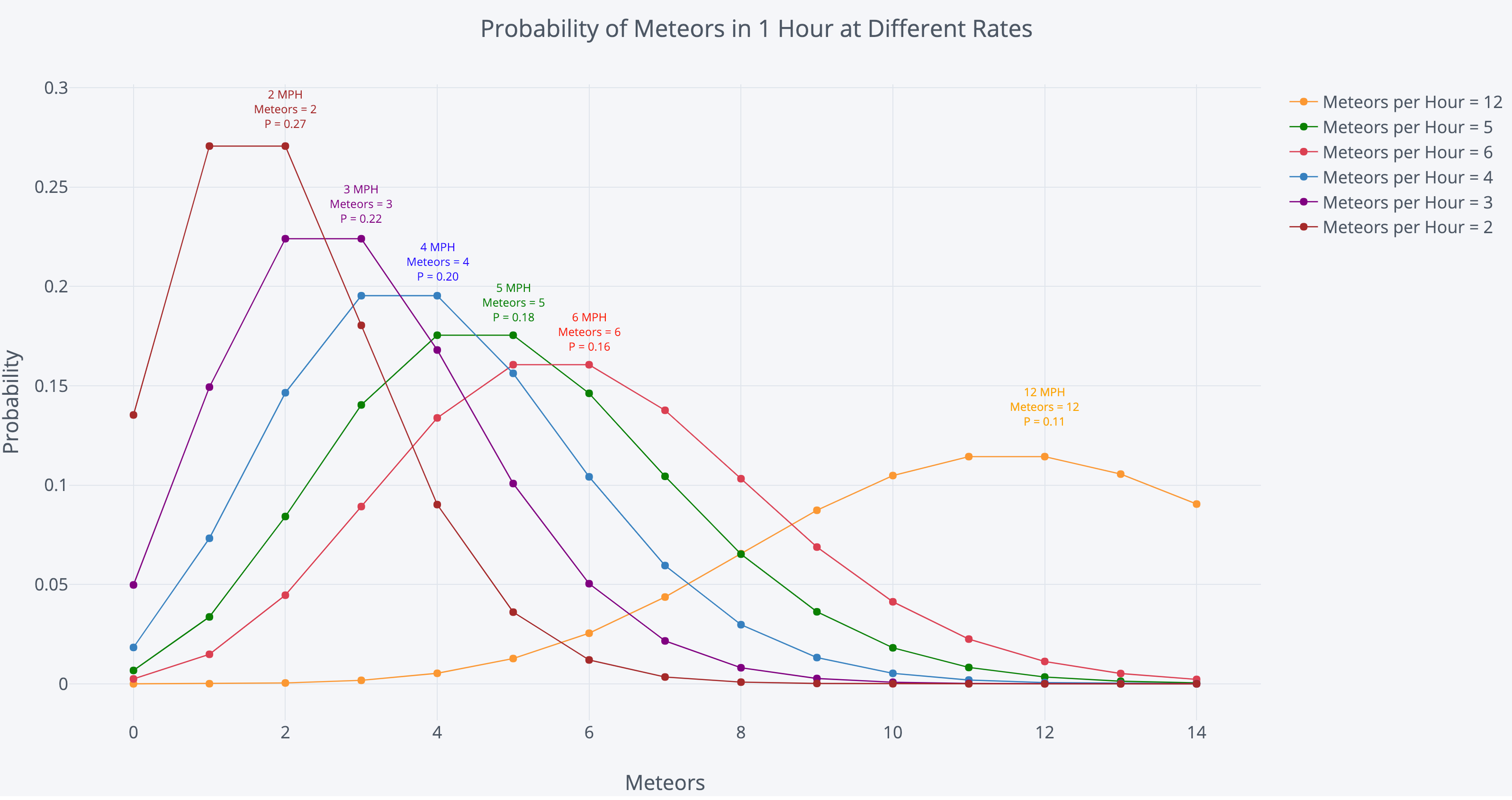
Poisson Probability Distribution Graph - Research Topics - Source quantitative-probabilitydistribution.blogspot.com
- Probability Mass Function: Determines the probability of observing a specific number of events.
- Mean and Variance: Equal to each other, representing the average number of events per unit interval.
- Parameter Estimation: Involves estimating the unknown rate parameter based on observed data.
- Hypothesis Testing: Used to test whether the observed data follows a Poisson distribution.
- Applications: Extends to areas such as queuing theory, insurance, and epidemiology.
- Assumptions: Assumes independence of events and a constant rate over time.
These key aspects provide a comprehensive framework for understanding and applying the Poisson distribution. It is a versatile tool for modeling discrete events, enabling researchers and practitioners to analyze data, make inferences, and solve practical problems in diverse fields.

Poisson Distribution, Poisson Process & Geometric Distribution | PPT - Source www.slideshare.net
Poisson Distribution: A Comprehensive Guide To Understanding Data With Discrete Events
The Poisson distribution is a fundamental probability distribution that describes the number of events occurring within a fixed interval of time or space and is commonly used in the analysis of data with discrete events. It is defined by a single parameter, lambda (λ), which represents the average rate of occurrence of the events. The Poisson distribution is often used in a variety of fields, including physics, biology, and economics, to model phenomena such as the number of phone calls received by a call center per hour or the number of defects in a manufactured product.
:max_bytes(150000):strip_icc()/Clipboard01-23850f297c19425b86aecdc1d560ad40.jpg)
Poisson Distribution Formula and Meaning in Finance - Source www.investopedia.com
The Poisson distribution is particularly important in the field of data analysis because it provides a way to model and predict the occurrence of discrete events. By understanding the Poisson distribution, researchers and practitioners can gain insights into the underlying patterns and relationships within their data and make more informed decisions.
For example, in the field of healthcare, the Poisson distribution can be used to model the number of patients arriving at a hospital emergency room per hour. This information can be used to optimize staffing levels and improve patient care.
In the field of manufacturing, the Poisson distribution can be used to model the number of defects in a manufactured product. This information can be used to improve quality control processes and reduce production costs.
Overall, the Poisson distribution is a powerful tool for understanding and modeling data with discrete events. By gaining a deep understanding of the Poisson distribution, researchers and practitioners can make more informed decisions and improve the effectiveness of their work.